Thermochemical Energy Storage Modeling

The motivation
Batteries are ubiquitous in our daily life. Most prominently, we use them to supply power to our cell phones and laptops because we do not have access to electricity 24/7, such as when we are travelling. We want the batteries to last as long as possible, so that we do not have to constantly charge them. Batteries are also extremely crucial in supporting the renewable energy sector. Renewable energy sources are often fluctuative, for example solar power that is only available during the day, wind power that is dependent on the existence of wind, etc. To meet the energy demands during those times when the renewable energy sources are not available, a reliable and long-lasting energy storage system is required.
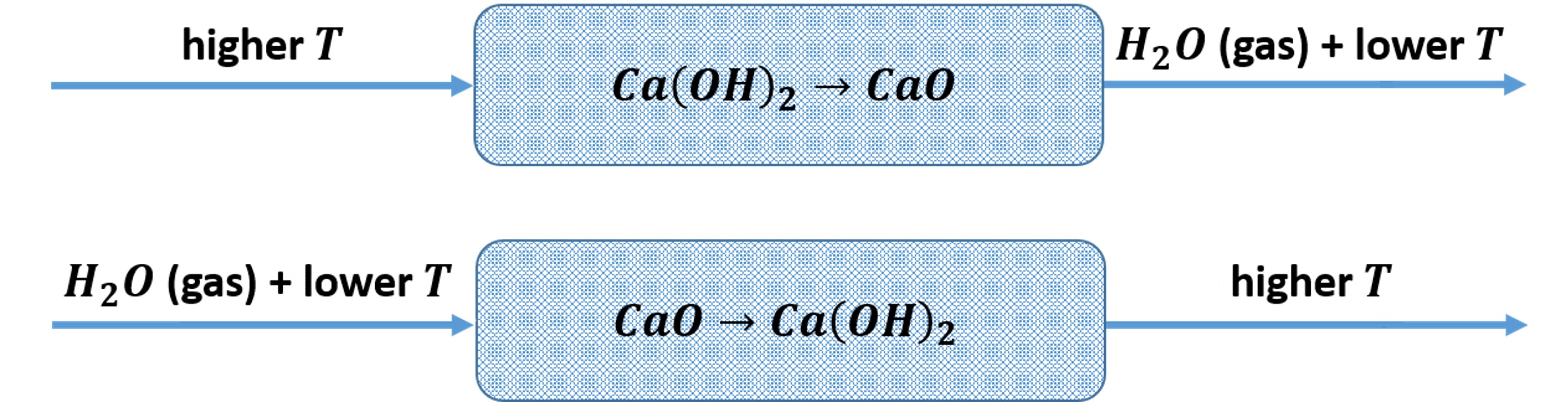
In this project, we considered a Thermochemical Energy Storage (TCES) system, shown by the sketch above. The device comprises of a calcium oxide - calcium hydroxide system. The charging process is performed by injecting dry air with high temperature into the device, resulting in the breakdown of calcium hydroxide into calcium oxide, releasing humid air at lower temperature. In a reversible manner, the heat can be discharged by injecting humid air with low temperature to compose calcium hydroxide from the calcium oxide, releasing the heat in the reaction process. The problem now, is that existing models of the TCES are computationally expensive, hindering a robust operational control of the system. Consequently, this system is not yet ready for commercial and industrial applications, and a faster yet accurate model is necessary.
Surrogate modeling using Physics-Informed Artificial Neural Network
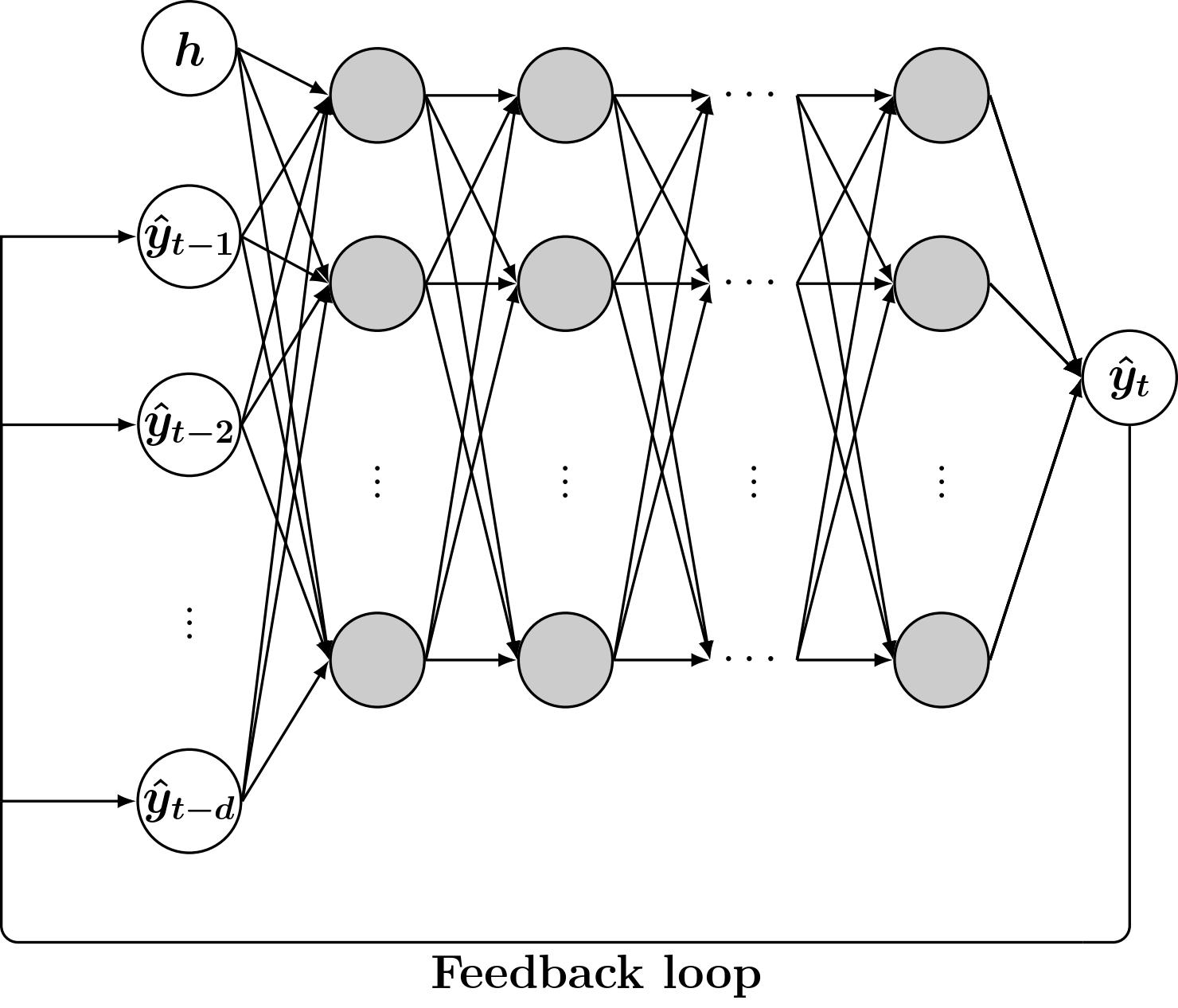
We used a Nonlinear Autoregressive Network with Exogeneous Inputs (NARX) as the model of choice. NARX is a type of recurrent neural network that solves a dynamic system, by taking the predicted values from earlier time steps to predict the corresponding value at the subsequent time step. This leads to a feedback loop as shown in the sketch below. NARX also provides a possibility to include additional inputs to the model. To improve the model accuracy and to make sure that the predictions are physically consistent, we also included several physics-based regularizations in the loss function definition. These additional regularizations include punishing the model if its prediction violates mass and energy conservation, if the temperature and the volume of calcium oxide are decreasing during the charging process (they should increase during charging and vice versa during discharge), etc.
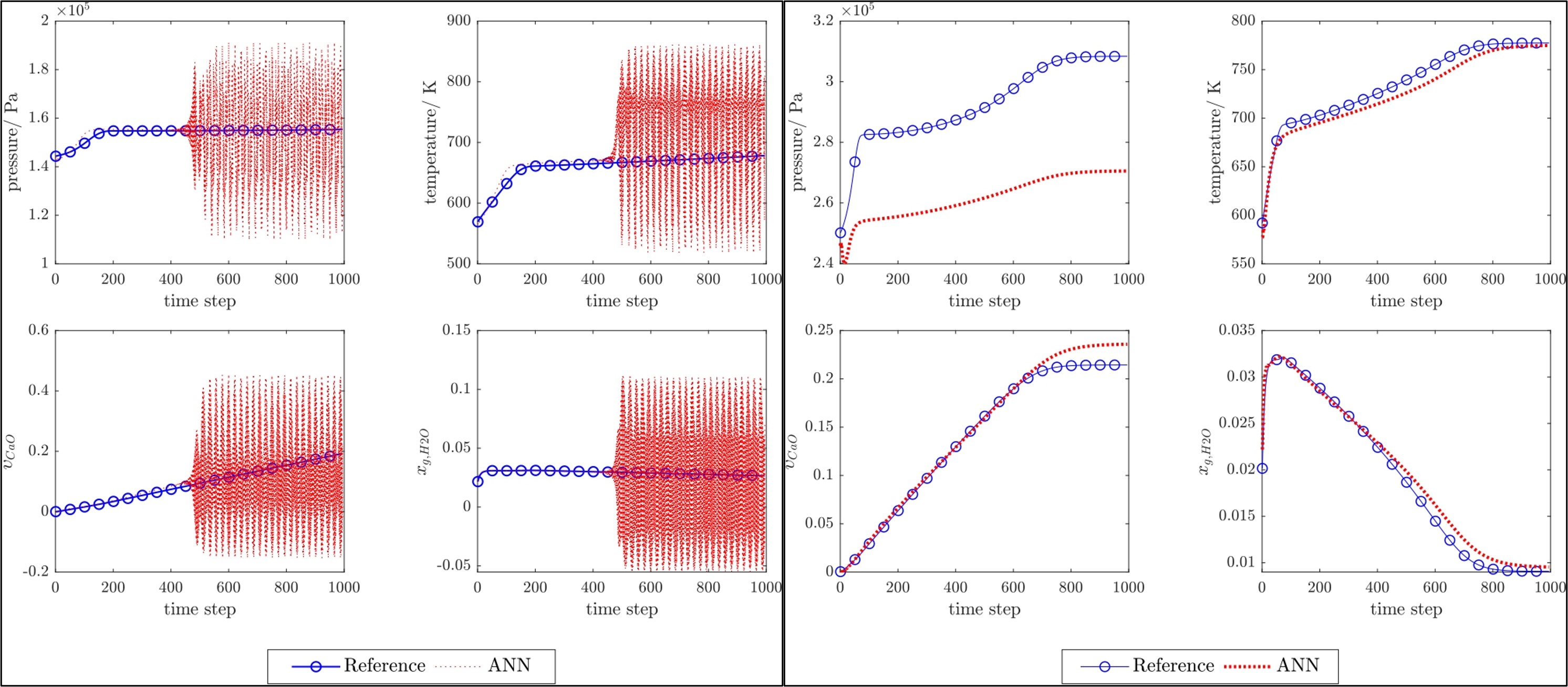
Do the physics-based regularizations help?
They do! To show that, take a look at the plots of the results below. For the comparison to be more evident and clear, we showed only the model predictions on a single data sample that possesses the highest error. The four plots on the left show the pressure, temperature, calcium oxide volume, and water content predictions obtained using NARX (the red lines) compared to the reference (blue lines). At its worst, NARX without the physics-based regularizations produces a highly erratic and erroneous predictions. On the other hand, the four plots on the right show that with the help of the regularizations, NARX's worst predictions are smooth and physically consistent, even though there are considerable errors like in the pressure predictions.
Investigating the importance of model inputs
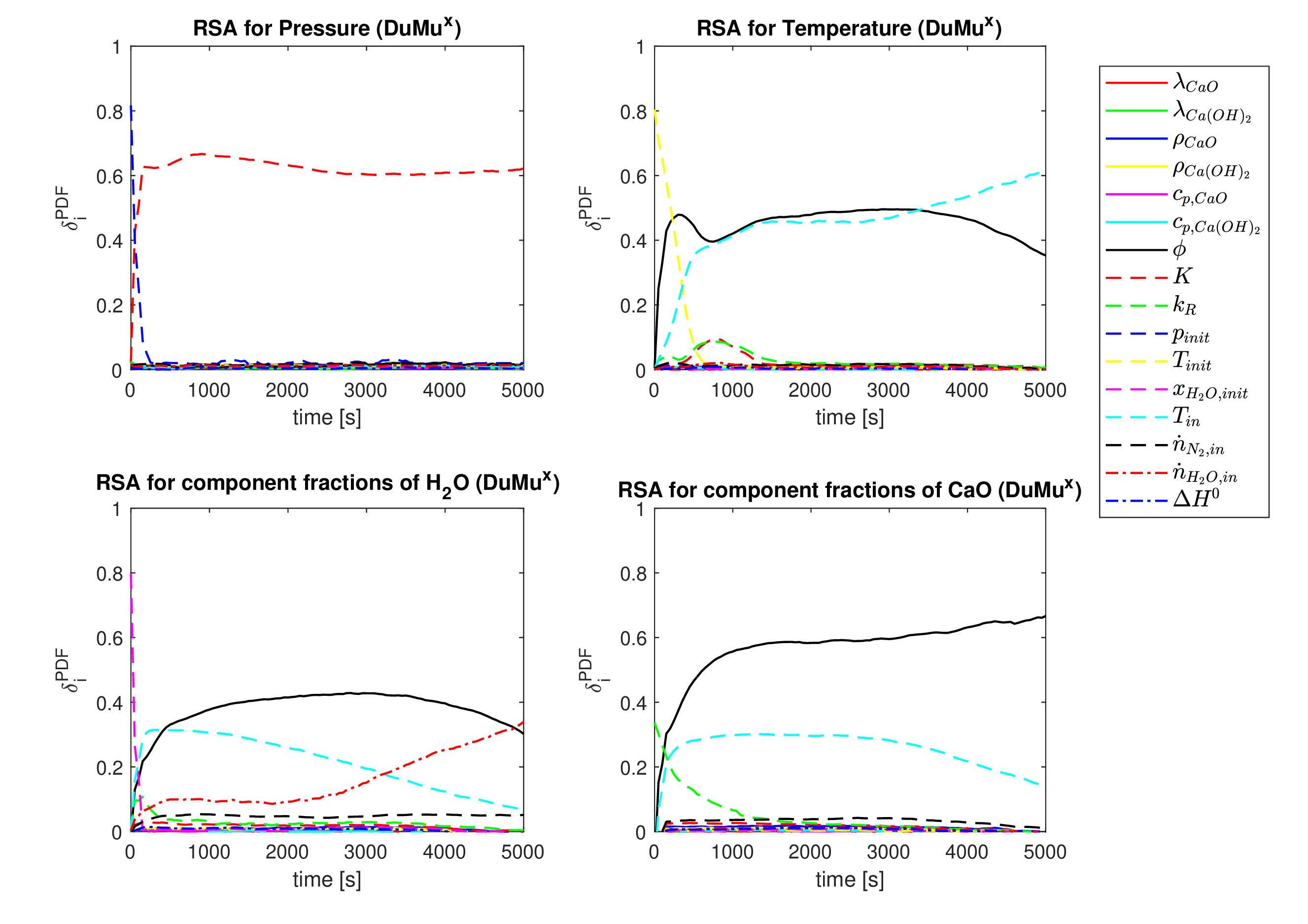
There is another issue with the NARX model that we discussed so far: it requires a lot of input variables (16 in total). Why is this a problem? Suppose that for a single variable, we need 10 data points for proper sampling. Now if we have two variables, we need a combination of 10 x 10 = 100 data points. For three variables, the combination grows into 10 x 10 x 10 = 1,000 data points. In short, the increase in the number of inputs leads to an exponential increase in the required number of data points to properly train the model. Additionally, more input variables equals a larger model with more parameters and higher computational time.
So, we investigated the importance of the model inputs using a global sensitivity analysis method, which also takes into account the dependencies and relationships between the inputs. This sensitivity analysis measures the effect of a change in the input parameters on the model output. If the model output is highly affected by a small change in a variable, then the corresponding variable is considered as a sensitive (important) parameter. Based on the results, we were able to narrow down the important parameters to only 8 instead of 16 (the variables with high sensitivity indices in the plots below). Future research can then focus on these 8 parameters, resulting in more efficient design experiments.
TLDR
In this project, we developed a surrogate model for the Thermochemical Energy Storage (TCES) system using a Nonlinear Autoregressive Network with Exogeneous Inputs (NARX). To improve the prediction accuracy and physical plausibility, we included physics-based penalties in the loss function to regularize the model physically. The addition of physics-based regularization improves the NARX prediction significantly compared to the one without. We also investigated the importance of all the model inputs, and found that 8 out of the total of 16 input parameters are important, and the rest could be excluded in the model development for future works.