Multiscale Modeling for Fractured Geothermal Reservoir

The motivation
An ideal geothermal reservoir needs three main factors: heat, fluid (water and/or steam) that transfers the heat, and permeability (hydraulic conductivity) that enables the fluid to flow to the production wells. To increase the heat production rate, it is therefore desired to exploit the fractures inside the reservoir, which are basically freeways for the fluid flow. However, the presence of fractures also comes with a caveat in the modeling process. Normally, the fractures inside the reservoir form a complex network which leads to a very heterogeneous system. Complex heterogeneous system needs a high resolution (read: expensive and computationally demanding) model for the prediction to be accurate. So the question is: can we build a model with low resolution but still accurate enough for fracture modeling purposes?
The multiscale method, a.k.a. the switch between coarse and fine scale
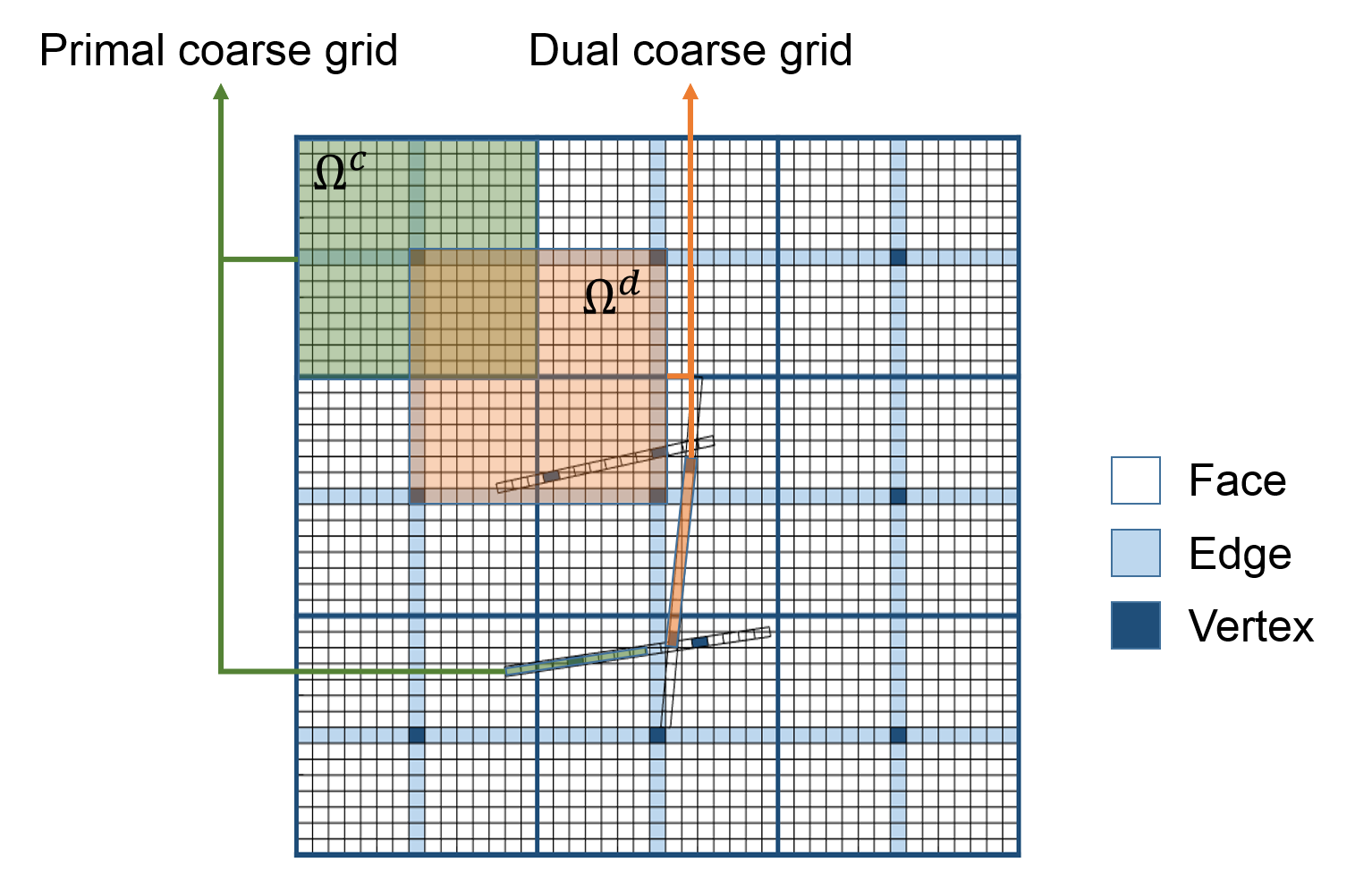
The short answer is: yes we can! First, the coarse representation of the reservoir is generated. In the sketch above, we have a reservoir that is represented by 45 x 45 fine grids. To simplify the model, we constructed coarse grids that contain 15 x 15 fine grids. As a result, instead of solving a 45 x 45 system (2,025 x 2,025 matrix), we only need to solve a coarse 3 x 3 system (9 x 9 matrix), which is a lot faster. Now comes the beauty of this method: after solving the system in coarse scale, the solutions can be reconstructed back into fine scale without losing too much accuracy!
As also shown in the sketch, two types of coarse grids are required: primal and dual. Each primal grid contains a single vertex that represents the volume average of all the 15 x 15 fine grids contained within it. The dual grid, on the other hand, is bounded by four vertices and it overlaps with the primal grids. The purpose of the dual coarse grids is to facilitate calculations of the connectivity between one primal grid and the others. To encode the fine scale details, basis functions are solved within the dual coarse grids. These basis functions are the most important element of the multiscale method, because they serve as the interpolators to switch back and forth between the coarse and fine scale solutions.
Coupling with the fractures
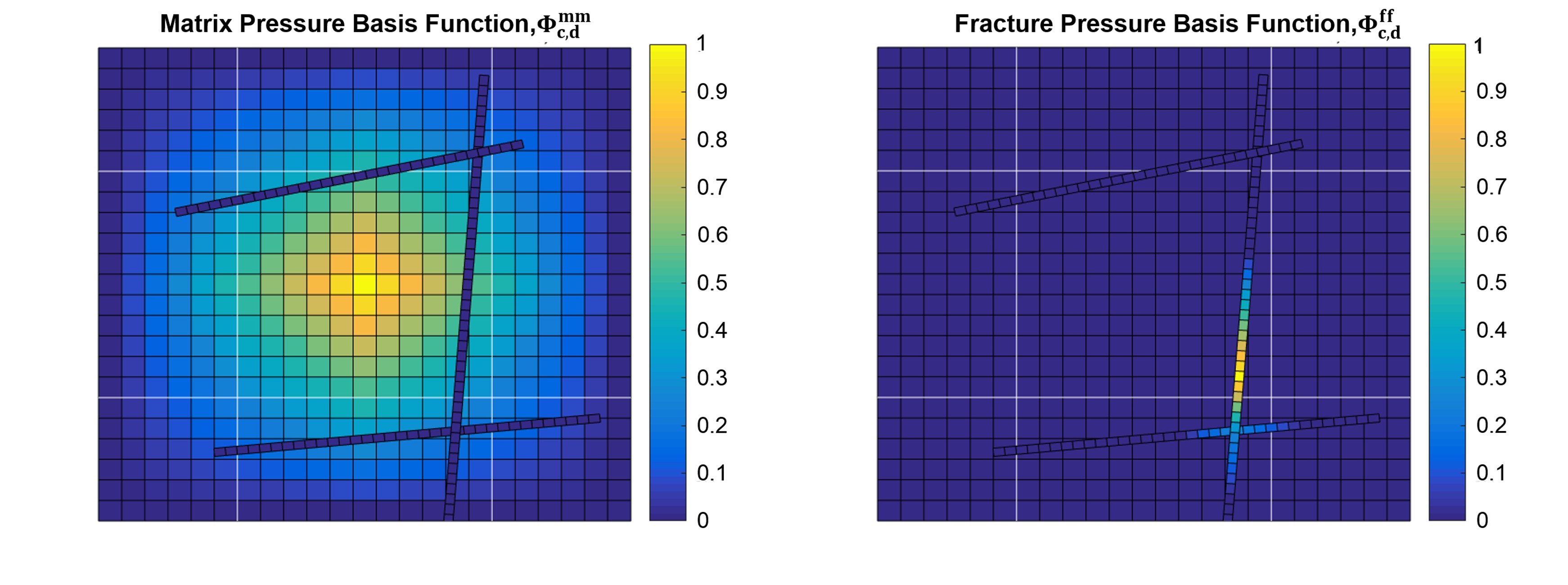
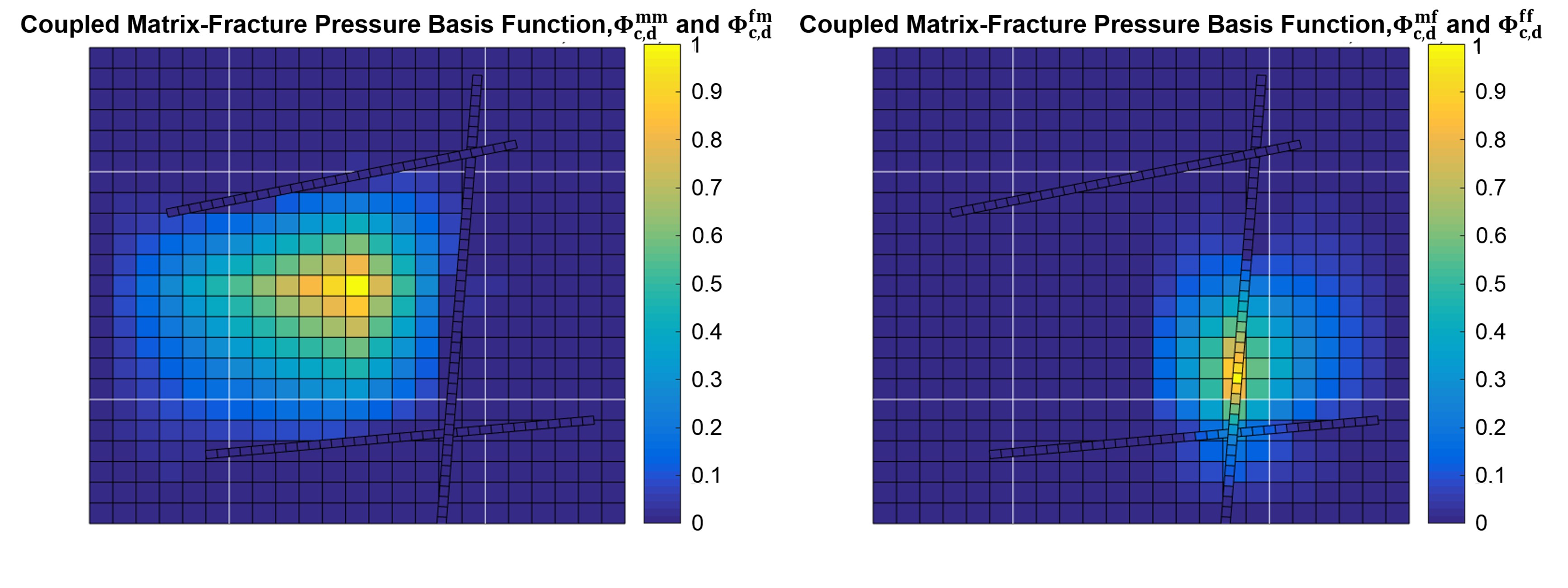
The basis functions are solved both on the matrix (the regular square grids in the sketch), and on the fractures (the thinner rectangular grids in the sketch). In this project, we considered two coupling approaches to solve the basis functions: the decoupled and semi-coupled approach. The decoupled approach assumes complete independence between the matrix and fracture domain, meaning that the basis functions in the matrix are not influenced by the presence of fractures, and vice versa (see the figures above). In the semi-coupled approach, basis functions are first solved inside the fracture domain without any influence from the matrix. Then, the basis functions inside the matrix are solved, taking into account the influence from the fracture basis functions (see the figures below).
The results
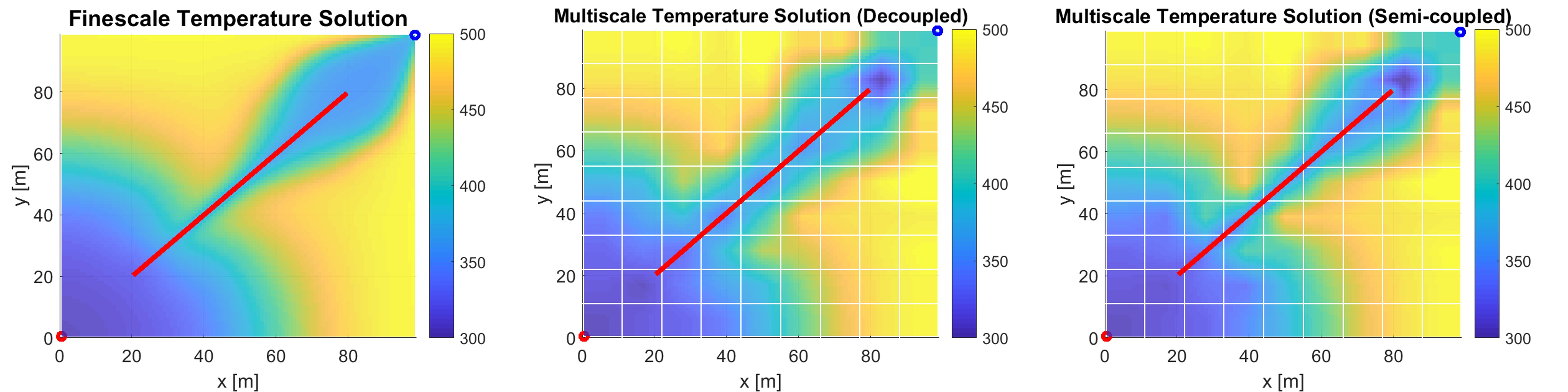
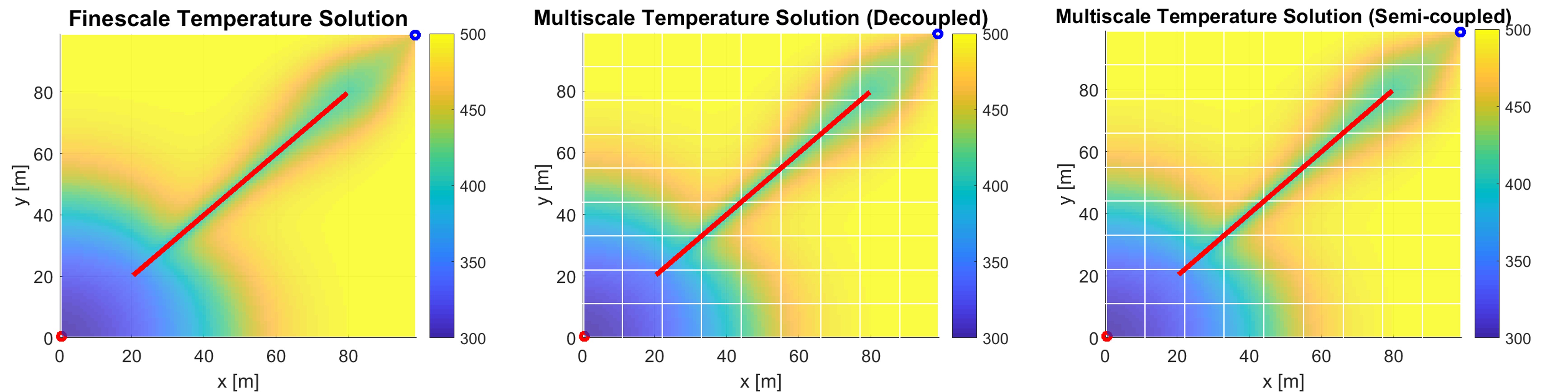
Now let's consider a simple homogeneous reservoir with only a single fracture. Cold water is injected from the bottom left corner (red circle at x = 0, y = 0) and water flows out through the production well (blue circle at x = 100, y = 100). The left plot above shows the fine scale temperature solution as reference, solved with 99 x 99 grids. The middle plot shows the multiscale temperature solution obtained using the decoupled strategy, and the rightmost plot shows the multiscale solution obtained with the semi-coupled approach. The multiscale solutions are solved only with 9 x 9 coarse grids (denoted by the white lines in the plot). Higher errors can be observed on the multiscale solution obtained using the decoupled approach, especially in the areas surrounding the fracture. This is expected, because the decoupled strategy ignores the matrix-fracture connection completely. However, with an additional smoothing stage using an ILU factorization, the multiscale solution errors are significantly reduced, as shown in the plots below.
How does the method perform on a more complex fracture network?
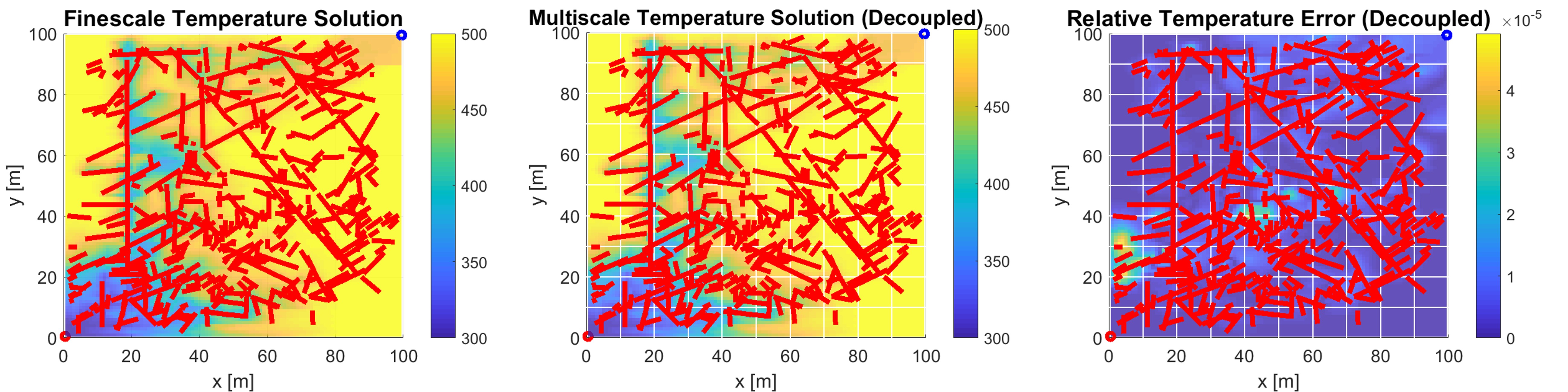
To answer this question, we considered a very dense fracture network, modeled based on an outcrop in Brazil. To add another layer of complexity to the modeling task, the hydraulic and heat conductivity of the reservoir are treated as heterogeneous. For this model, we implemented the decoupled multiscale approach for maximum computational efficiency. The results are shown in the plots below, with the relative error on the rightmost plot, showing reasonable accuracy of the multiscale approach, with notable errors only in small areas that are not very relevant to the fluid flow path.
TLDR
In this project, we introduced a multiscale modeling approach to solve both pressure and temperature in fractured geothermal reservoirs. With the multiscale method, a model can be solved more efficiently on a coarse scale without compromising the fine scale details. More interestingly, the coarse scale solution can be interpolated to reconstruct the fine scale solution with high accuracy using the basis functions. We successfully applied this method on a complex fracture network model, based on real geological outcrop data. Further developments of the model could include a multiphase flow inside the reservoir and geomechanical effects (such as fracture activation, closure, and propagation).