PDE Benchmark for Scientific Machine Learning
The motivation
Machine learning predictions on image classification tasks have improved significantly during the past decade. One of the most important drivers for the breakthrough in this field is the availability of popular benchmarks. These benchmarks, such as MNIST, CIFAR-10, and ImageNet, facilitate a standardized way of evaluating and comparing machine learning models. Such benchmarks, unfortunately, are still missing in the field of scientific machine learning to solve physical problems. This project is intended to provide diverse datasets of various well-known Partial Differential Equations (PDEs), along with the codes for data generation and model training to make the benchmark easily extensible.
The dataset and baseline models
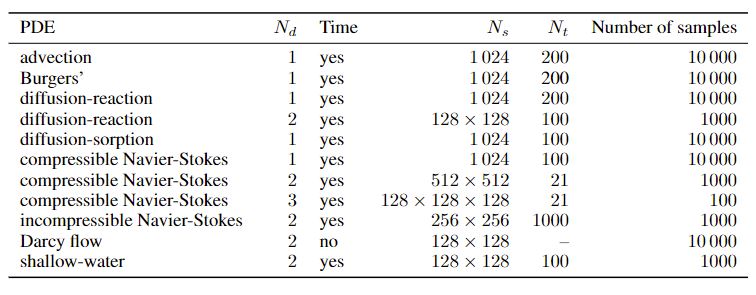
In this benchmark, we provided datasets based on various PDEs, ranging from 1 to 3 dimensions in the spatial domain. The 1D datasets are generated with 1,024 grids and 10,000 samples each. The 2D datasets are generated either with 512 x 512, 256 x 256, or 128 x 128 resolution, depending on the number of time steps, and the computational demand of each corresponding problem. There are 1,000 samples associated with each 2D dataset. The 3D dataset is generated with 128 x 128 x 128 resolution, and 100 samples are available. The table below shows the overview of the datasets provided in this benchmark. Regarding the baseline models, we chose U-Net and FNO that are capable of modeling spatiotemporal problems. More importantly, we also included PINN as the representative of physics-informed machine learning model.
Baseline models comparison with the traditional PDE solver
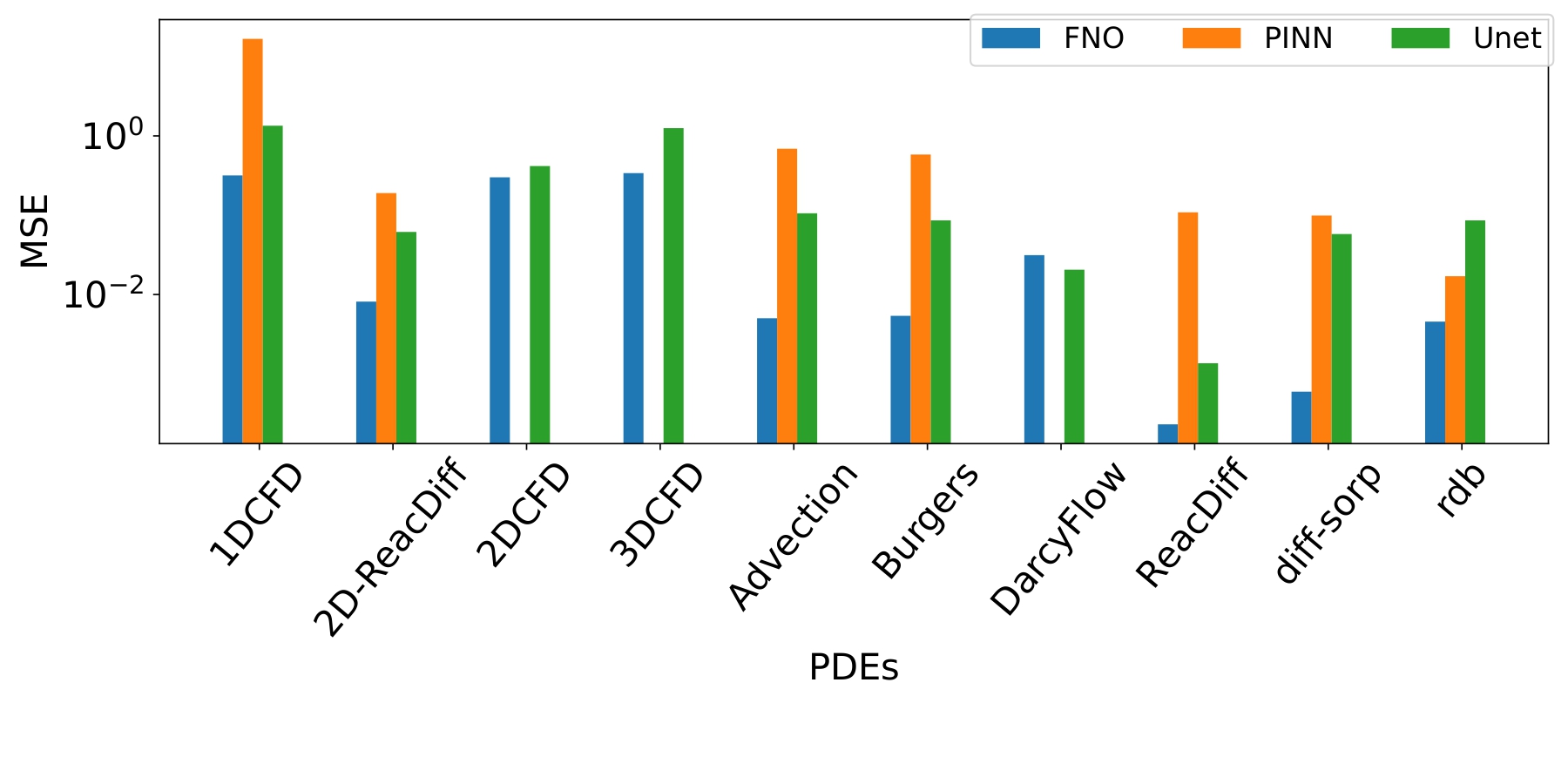
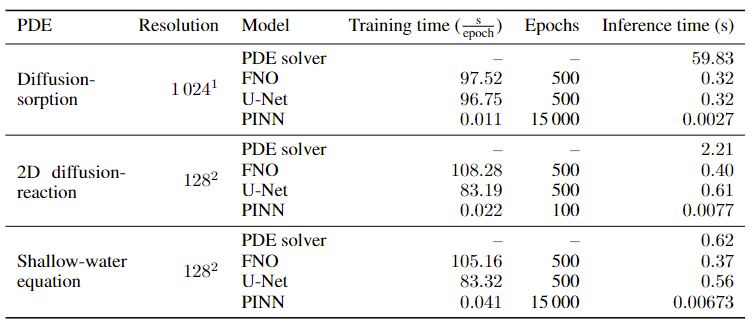
The bar chart above summarizes the comparison of prediction errors between the three baseline models. Among the three models, FNO produces the most accurate predictions in almost all cases. Interestingly, PINN's predictions are not as accurate as FNO and U-Net, indicating that further works in the physics-informed machine learning direction are indeed necessary. Another important thing to compare is the training and inference time of the baseline models. Many scientific machine learning applications are focused on surrogate modeling, which demands for a faster model. As shown in the table below, the training of the baseline models are computationally very demanding. However, once the training is finished, all of the baseline models are faster by multiple orders of magnitude during inference, compared to the traditional PDE solvers that were used to generate the datasets.
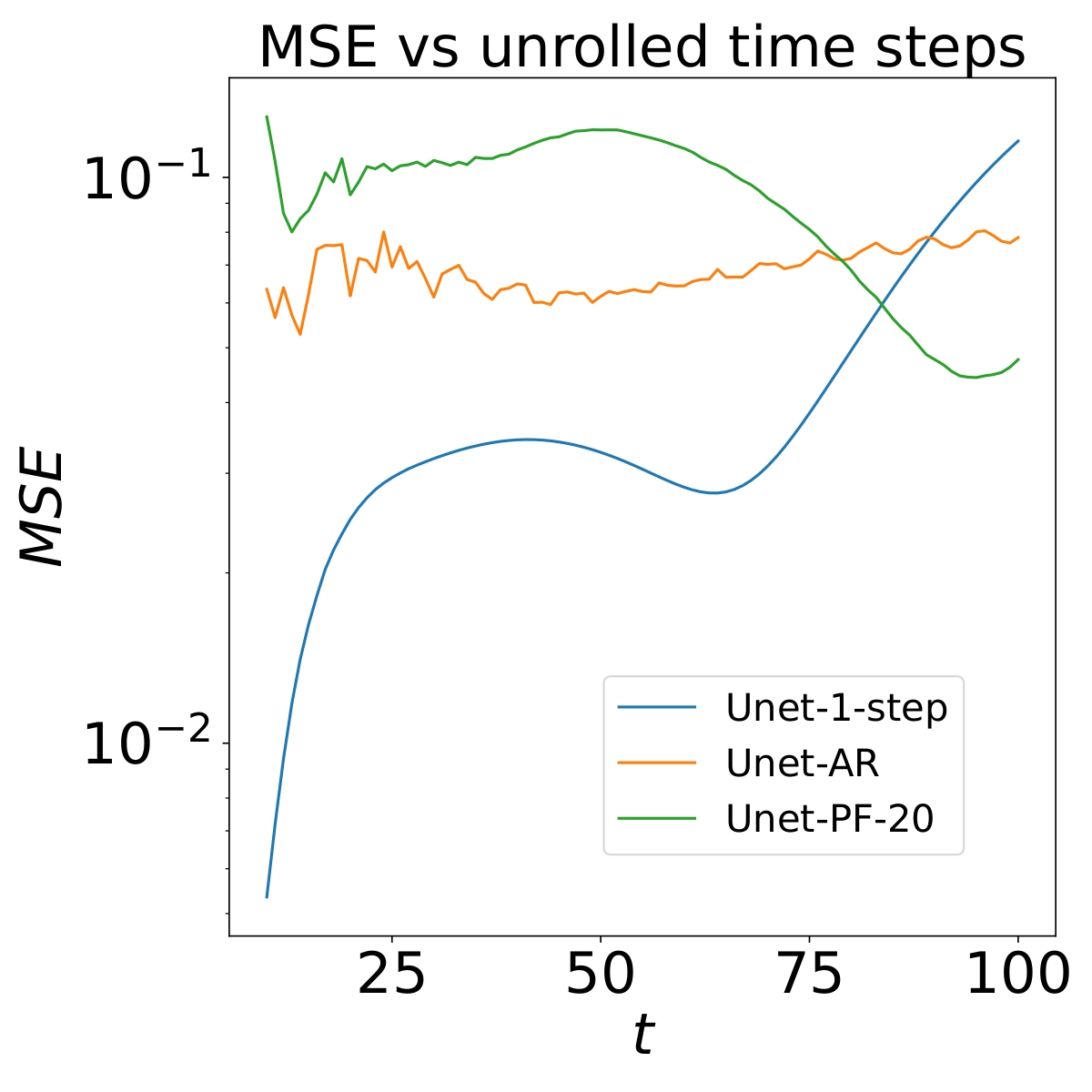
Temporal error behavior of the baseline models
When setting up the baseline models, we observed interesting temporal behaviors. When training U-Net in a fully autoregressive mode, major instabilities were observed. To prevent the instability, we set up the U-Net baseline similarly to FNO: it takes multiple time steps as the initial condition. In addition to that, we tested three different training modes for U-Net: 1 time step ahead, pushforward trick, and fully autoregressive. The 1 time step ahead training mode allows for a very stable training, but it leads to high error accummulation with more unrolled time steps during testing. The pushforward trick backpropagates the gradient information only up to several time steps, and it also improves stability during training. The fully autoregressive mode backpropagates the gradient all the way to the initial input, leading to a less stable training. It is also very interesting to observe from the plot below, that the pushforward trick seems to have a decreasing error with more unrolled time steps, producing predictions with the lowest error compared to the other training modes. A more detailed analysis on this phenomenon could be investigated in future works, to improve model predictions on a longer prediction horizon.
TLDR
With this PDE benchmark, we contributed an extensive dataset collection and baseline models setup for the scientific machine learning community, covering 1 to 3 dimensional problems. We provided our source codes that can be used to generate more datasets, to train the baseline models with new datasets, and even to add new baseline models to the benchmark. We also provided solutions to the training stability that we encountered, and we introduced an interesting temporal behavior of the baseline model predictions as a result of implementing these solutions. This behavior can be analyzed in future works to improve model performance on longer prediction horizon. The scope of our benchmark is currently only limited to mostly fluid flow problems. Other types of physical problems can be further included in an extension to this benchmark.